学递归,跳不过汉诺塔这个程序。以前弄NOIP,老师很详细地讲过汉诺塔的原理以及实现算法,不过我上大学了却发现老师讲到汉诺塔,只是像一笔带过,原理都没讲通,更别说算法了。我相信像他那么讲,没一个同学(没基础的)能弄得懂,就算你给一个flash汉诺塔的游戏,也不见得会玩。
汉诺塔真的挺有意思的,我写这篇文章,也算是回忆回忆以前学过的知识。如果有什么错误,还请原谅。
没有听说过汉诺塔的人,可以去baidu查查,或则你去http://www.4399.com/flash/293.htm 玩一玩,大概就知道是干什么的了。
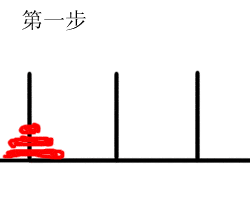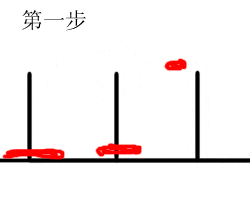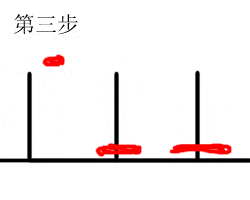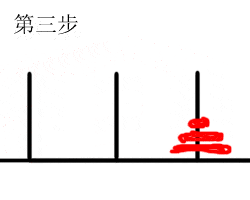
现在有A、B、C三根柱子,A柱子上有n个大小不同的盘子,准备移到C柱子上。我们现在换一个说法:A柱子上有n个大小不同的盘子,我们借助B,将A上的n个盘子移动到C上。
假设n是1,很简单,直接将A上的1个盘子移到C上。
假设n是2,怎么想?分三步,一是将小盘子移到B上,二是将大盘子移到C上,三是将小盘子移到C上。在大盘子移到C上之前,小盘子在哪里都无所谓。
所以我们先将小盘子从A上移到B上,再把大盘子从A移到C上,再把小盘子从B移到C上。移完后总共需要移动的次数是3。
假设n是3,分三步,一是把上面的两个盘子借助C移到B,二是把大盘子移到C,三是将其余两个盘子借助A移到C。其中第一、第三步又分两个小步。这两步步骤和n=2时相同,所以移完后总共需要移动的步数是3+1+3=7步。
我们已经可以从其中发现递归的思想。当我们做第一步时,完全可以忽略最大的盘子,问题仅仅是将两个盘子从A借助C移到B。第三步时,也忽略已经移到C柱子上的大盘子,问题变成将在B上的两个盘子借助A移到C。
于是我们可以设计一个函数,它的功能是将n个在x柱子上的盘子借助y柱子移到z柱子上。
这么写:hanota(n,x,y,z);
于是我们上面的三步可以用程序语言来表达:
- hanota(n-1,A,C,B);
- hanota(1,A,B,C);
- hanota(n-1,B,A,C);
这是三个盘子时候的情况。四个盘子时候我们仍然可以这样想,先将上面的三个盘子借组C移动到B,再将最下面一个盘子移动到C,最后将其余三个盘子借助A移动到C。然后一、三两步又分两个小步。通过递归的思想,将大问题逐步转化成小问题。最后解决。
下面看我们这个hanota函数怎么写。
#include<stdio.h> void hanota(int n,char x,char y,char z){ if(1 == n) printf("将%c上的盘子移动到%c柱子上\n",x,z); else{ hanota(n-1,x,z,y); //第一步 printf("将%c上的盘子移动到%c柱子上\n",x,z); //第二步 hanota(n-1,y,x,z); //第三步 } } int main(){ int n; printf("输入盘子的数量:"); scanf("%d",&n); hanota(n,'A','B','C'); return 0; }
我们看这个递归,最后的结束条件是n==1时。也就是说问题大而化小之后,只有一个盘子了,就可以直接移动了。否则就继续将n-1放进hanota函数进行移动(也是三步)。
这是移动三个盘子的结果图,和我上面的那个gif里移动的步骤是一样的。你们也可以试一下,不过输入的n不能太大了,否则算不出来的。移动的步数和n是成指数增加的,当n=64时,需要移动2<sup>64</sup>-1次,这是个天文数字。n通常不要大于16就行了。
如果你以前没有任何递归的基础,也许你看不懂这些代码。如果你知道递归的一些知识,你才会发现这道题实际上十分基础。但是如果不用递归来做,我想没多少人能把程序写出来。因为递归解决了我们很难思考的问题,将问题大而化小。很多新手包括我有时候在想,递归明明好像比循环难,但为什么老师说递归更易于理解。这些东西也许只有等我们做了更多题,接触了更多有关树和图的问题以后才能理解吧。
最后给大家和我自己留一个问题:汉诺塔是三根柱子,如果我们有四根柱子,我们又怎样移动盘子,或者说怎样移动使步数最少?有时间我会想想这个问题,以后写一个“汉诺塔拓展”。
我把程序传到附件里了,大家可以下载运行了试试。